INTERSEZIONE INVERSA O PROBLEMA DI SNELLIUS-POTHENOT
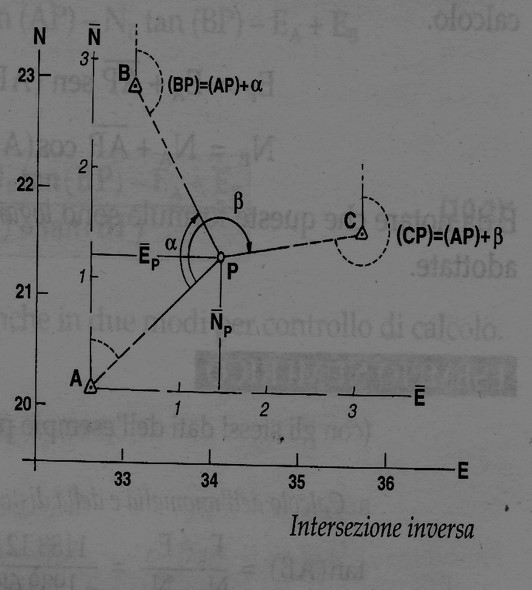
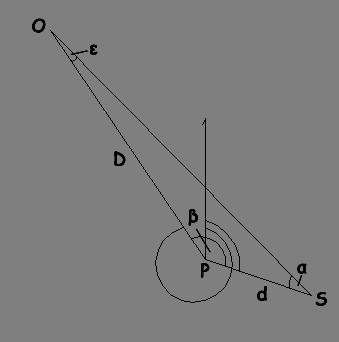
Il punto P viene determinato utilizzando tre direzioni interne non orientate PA, PB e PC, verso tre punti noti A,B,C ricavando, pertanto, gli angoli α e β.
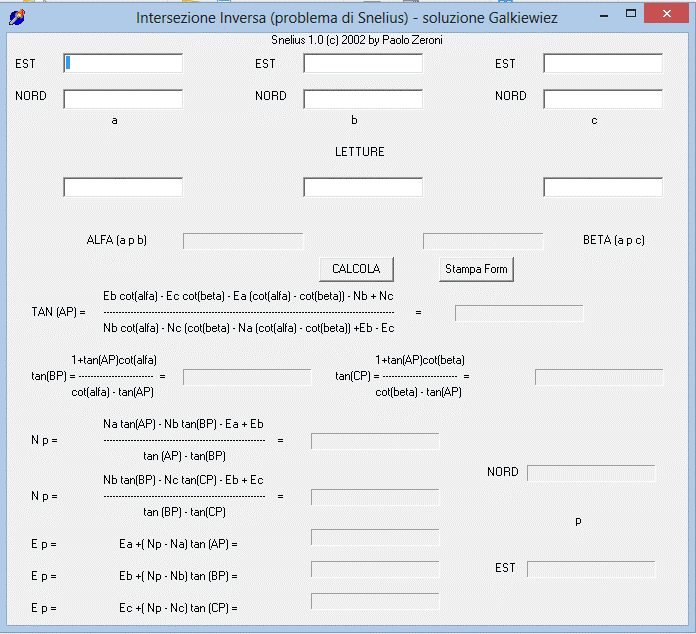
Ci sono diverse soluzioni a questo problema ma, oggi, grazie all’uso dei calcolatori elettronici, si preferisce usare la soluzione detta del Galkewiez :
Si calcola prima di tutto (AP) con la formula :
Eb cot α – Ec cot β – Ea(cot α – cot β) – Nb + Nc
tan(AP) = —————————————————————–
Nb cot α – Nc cot β – Na(cot α – cot β) – Eb + Ec
si riporta al quadrante (AP) e Si calcolano poi
(BP) = (AP) + α e (CP) = (AP) + β.
Oppure, senza riportare al quadrante :
1+ tan(AP) cot α 1+ tan(AP) cot β
tan(BP) = ———————– tan(CP) = ———————–
cot α – tan(AP) cot β – tan(AP)
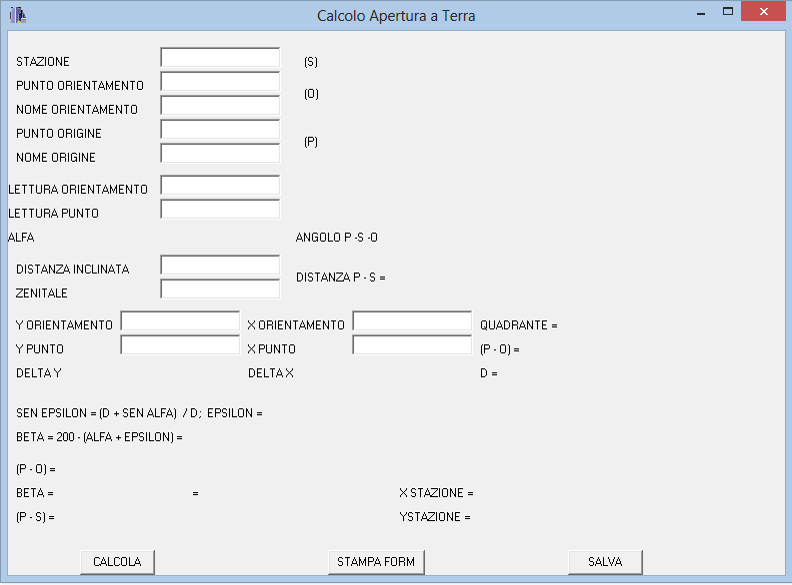
nella sezione download è presente una piccola utility per risolvere il problema.
Ecco una schermata :